With the coronavirus pandemic currently sweeping the globe, most of us here in Montréal are shut at home. But social distancing hasn’t kept my friends and I from discussing cool math (some school-related, some not) over videochat. The subject of today’s article is a little exercise that Prof. Luc Devroye gave some of us in his virtual office hours yesterday. After thinking on it overnight and working it out on paper this morning, I found a solution that I thought was pretty nice.
Bit sequences
The exercise went as follows. Starting with a sequence of $k$ bits (either $0$ or $1$), we repeatedly add a bit to the end and lop off a bit from the beginning. Each time we do so, we get a new $k$-sequence. Is it possible to cycle through all $2^k\!$ possible bit-sequences in this manner, in exactly $2^k\!$ steps? The answer is yes, as we shall soon prove.
As always, it is instructive to work out a couple small examples. When $k=1$, this is very easy, because we can start with $0$ and then replace it with a $1$. For $k=2$, we might start with the sequence $00$. Adding a $1$, we obtain the sequence $01$. Now adding a $0$, we get $10$. But here we’re stuck, because whether we add $0$ or $1$, we’ll get a sequence we’ve already seen. The correct thing would have been to add a $1$, giving us $11$, and then a $0$, giving us $10$. All $2^2 = 4$ sequences of length $2$ have been obtained.
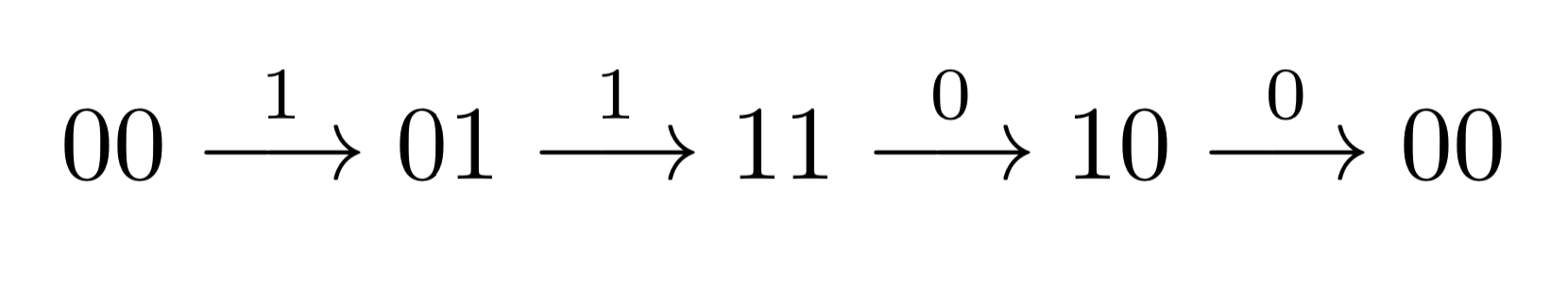
So we know that the statement is true for $k = 1$ and $2$. But of course, for larger values of $k$ we don’t want to be stuck guessing and checking, so we will have to develop a proof that works for all $k$. To this end, we need to introduce a couple of concepts from graph theory. (Feel free to skip the next section if you’re already acquainted with graphs.)
Graphs and cycles
Graph theory is the study of networks consisting of vertices (also called nodes) and edges between them. Often we have edges that are undirected in that one can travel along them in both directions, but our graphs will be directed, so every edge can be seen as a one-way street. For this article, we are concerned with cycles in a graph, i.e. paths that start at a vertex, travel around for a bit along edges, then return to the starting vertex.
Some natural questions to ask about graphs are as follows:
- Starting at a vertex, is it possible to traverse the graph using every edge exactly once and return to the starting point?
- Starting at a vertex, is it possible to traverse the graph hitting every node exactly once and return to the starting point?
In fact, an instance of the first question is one of the earliest problems in graph theory, and was solved by Leonhard Euler in 1736. In his honour, a cycle that uses every edge exactly once is called an Euler tour, while a cycle that visits every vertex exactly once is named a Hamiltonian cycle, after the Irish mathematician William Rowan Hamilton.
Although these questions about graphs seem very similar, the first is very easy and the second is very hard. It turns out that a graph has an Euler tour if and only if every vertex has as many edges coming in as going out. I won’t give the proof of this, but if you work out a couple examples, you might see why. Having an Euler tour means that it is impossible, in some sense, to “get stuck” by following an edge into a vertex and then having no way out. If every vertex has the same number of in-edges as out-edges, this can’t happen.
Representing bits as graphs
Graphs are relevant to our problem because we can represent the operation of adding a new bit to the end and dropping one off the beginning as a walk in a graph. For any $k\geq 1$, we can create a graph with $2^k$ vertices, representing all possible $k$-sequences of bits. Then we draw an edge from a vertex to another if it is possible to go from one sequence to the other with exactly one bit-adding operation. We let $G_k$ denote the graph representation for the $k$-sequence problem; here are $G_1$ and $G_2$:
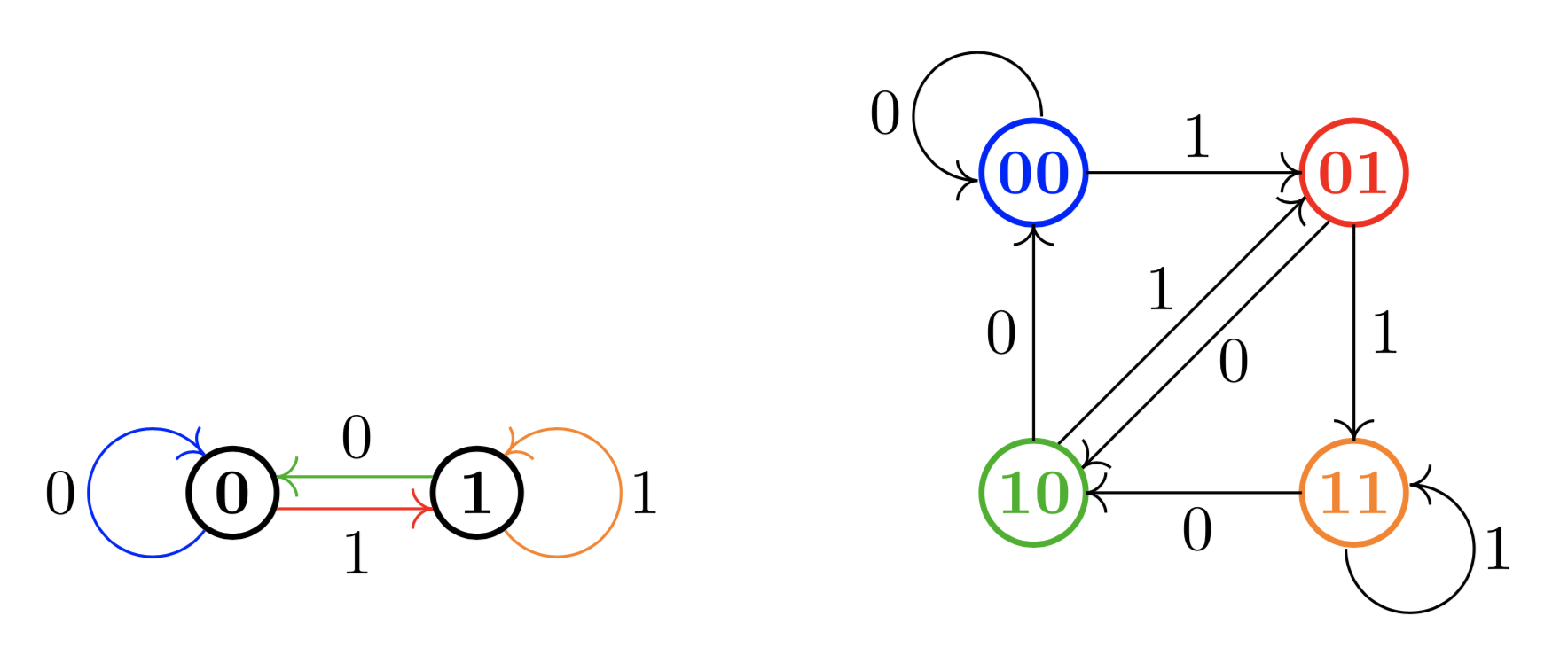
Now it is clear why we have represented the sequences in this way. The original problem asked us to cycle through all $2^k$ possible bit-sequences by performing the bit-shift operation one at a time. This reduces to the problem of finding a Hamiltonian cycle in the graph representation. However, like I said earlier, proving the existence of Hamiltonian cycles isn’t as easy as finding Euler tours. So it isn’t immediately obvious that for any $k$, the graph representing $k$-sequences should have a Hamiltonian cycle.
From Euler to Hamilton
However, we note that every vertex has exactly two edges leading out (corresponding to adding either a $0$ or a $1$) and two leading in from other sequences. This means that for all $k$, $G_k$ has an Euler tour! This wouldn’t help us, except that we can draw a correspondence between the edges of $G_k$ and the vertices of $G_{k+1}$. The correspondence runs as follows:
If an edge, labelled with a bit $b\in \{0,1\}$ in $G_k$ connects vertices $u$ and $v$, then we create a vertex in $G_{k+1}$ with the same label as $u$, but with the extra bit $b$ added to the end. This is illustrated in the diagram above, where the four edges in $G_1$ correspond to the four nodes in $G_2$. Then we draw an edge between nodes $a$ and $b$ in $G_{k+1}$ if and only if in the original graph $G_k$, the destination of the edge corresponding to $a$ is the starting point of edge $b$. This is less complicated than it sounds when you look at the picture. As an example, the orange node connects to the green one in $G_2$ because in $G_1$, the orange arrow leads to a node that the green arrow starts from.
Notice that an Euler tour in $G_k$ is exactly a Hamiltonian cycle in $G_{k+1}$! Because we know that every $G_k$ has an Euler tour for all $k\geq 1$, we know that for all $k\geq 2$, $G_k$ has a Hamiltonian cycle ($G_1$ does as well, but we can check that manually).
Back to bits
We now have a way to read off the bit sequences that solve the original problem. $G_1$ and $G_2$ give us the solutions for $k=2$ and $k=3$ respectively:
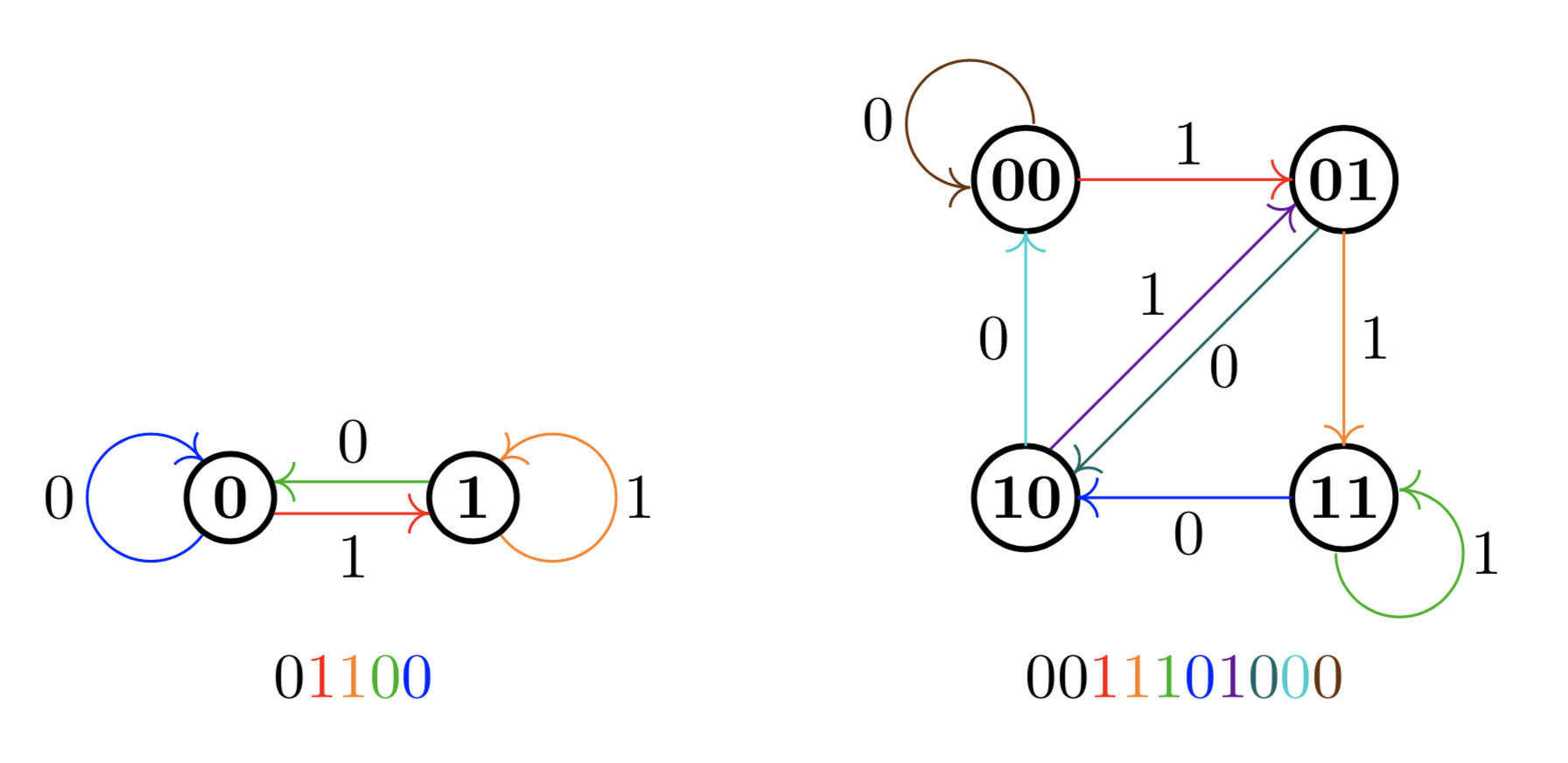
The bit sequences at the bottom contain every possible $k$-sequence as a substring and each corresponds to an Euler tour of $G_{k-1}$. Neat!
Links and references
I later found out that the sequences above are called de Bruijn sequences and the graphs are called de Bruijn graphs. So the solution I found is quite well-known (it’s in the Wikipedia page I just linked). The construction of taking a graph and producing another graph whose vertices correspond to the edges of the original is detailed in Donald Knuth’s The Art of Computer Programming, Vol. 1, in an exercise on oriented trees (Section 2.3.4.2, Exercise 21).
A postscript on PostScript. I drew the graphs above by hand-coding them in PostScript. Click for the source code of the first one, and of the second one.